Programmation structurée
Contenu


6. Programmation structurée¶

%matplotlib inline
import numpy as np
from IPython.display import HTML,display,IFrame,Video
from IPython.display import YouTubeVideo,Markdown
Astuce
pour tester les programmes Python, vous pouvez vous connectez sur un serveur Jupyter, par exemple, pour les étudiants Lyon1 https://jupyter.mecanique.univ-lyon1.fr
6.1. Programmation structurée¶
En Informatique il existe différentes méthodes de programmation ou paradigmes de programmation (programmation structurée, programmation orientée objects, programmation fonctionnelle…). Parmi ces paradigmes, la programmation structurée est une méthode simple et disponible dans de nombreux langages de programmation scientifique (Python, C, C++, ..). Le principe de base est le suivant:
principe:
Divide and Conquer
qui consiste à découper le problème en une suite de problèmes plus simples
6.1.1. Analyse algorithmique « Top-Down design »¶
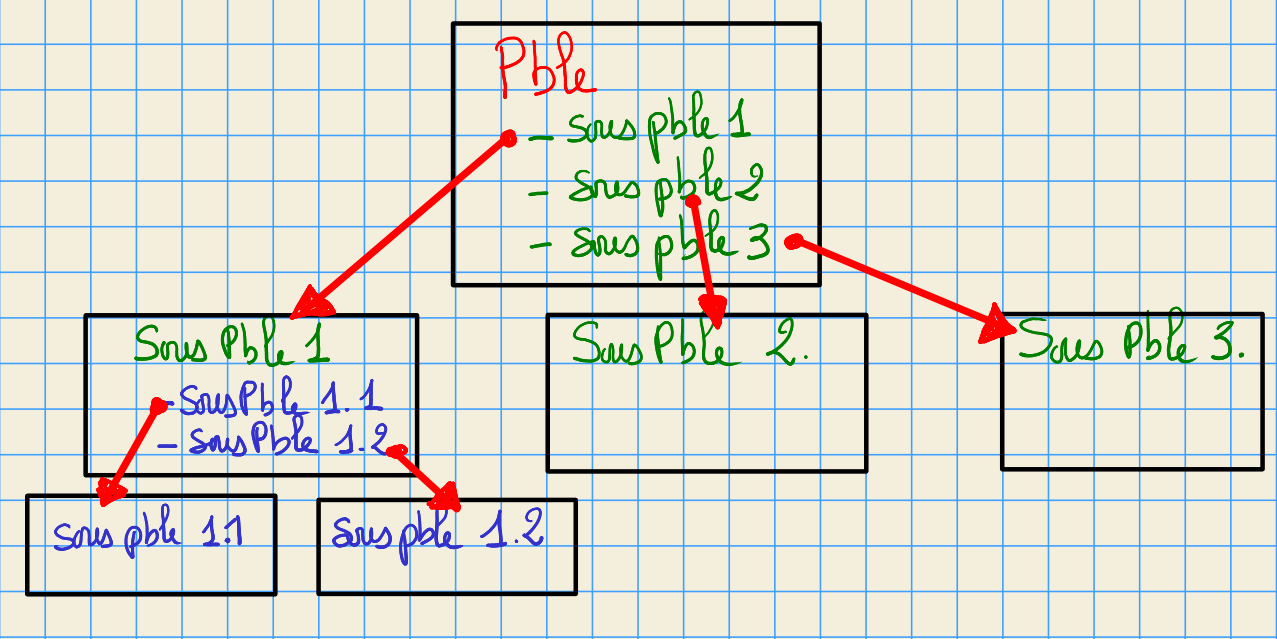
6.1.2. Principes de l’analyse top down¶
on découpe le problème en une série de sous-problèmes plus simples (si possible indépendant)
on spécifie ce qui doit résolu dans chacun des sous-problèmes sans forcément dire comment
puis on itère au niveau des sous problèmes.
6.1.3. Programmation « Botton-up programming »¶
on part des sous-problèmes élémentaires que l’on programme sous forme de fonctions (ou procédures)
on valide les fonctions
puis on réitère en remontant dans l’arbre jusqu’au programme principal
règles réutiliser les fonctions déjà écrites et validées (bibliothèques): principe du moindre effort !
6.2. Exemple: simuler l’alunissage de Neil Amstrong (Apollo 11)¶
basé sur une simulation d’alunissage du module lunaire écrit en basic en 1969, puis popularisé en 1979 sur ATARI (Lunar Lander).
display(Markdown("**Video du cours: Programmation structurée sur un exemple 'Lunar Lander'**"))
YouTubeVideo('7QGM_BtCxRE')
Video du cours: Programmation structurée sur un exemple 'Lunar Lander'
Attention
Les vidéos utilisent un ancien interpréteur python 2.7, pour lequel print est un mot clé,
soit print 'bonjour'.
Avec Python 3, print est une fonction et il faut donc utiliser des parenthèses,
soit print('bonjour')
6.2.1. jeu « Lunar Lander »¶
Poser le module lunaire (LEM) sur la lune en arrivant avec une vitesse quasiment nulle. Pour cela on dispose de rétro-fusées permettant de ralentir la chute du LEM.
On contrôle manuellement ces rétro-fusées en sélectionnant une poussée (de 0 à 9), correspondant à l’éjection de carburant avec un débit \(Qe\) variable et une vitesse \(Ue\) fixe.
Mais on dispose d’une quantité limitée de carburant que l’on doit utiliser avec modération pour pouvoir atterrir en douceur.
6.2.1.1. modèle physique:¶
Le LEM, de masse initiale \(M0\), est soumis à la gravité \(g\) de la lune et à la poussée des rétro-fusées, correspondant à l’éjection d’un débit de fuel \(Qe\) à un vitesse \(Ve\) .
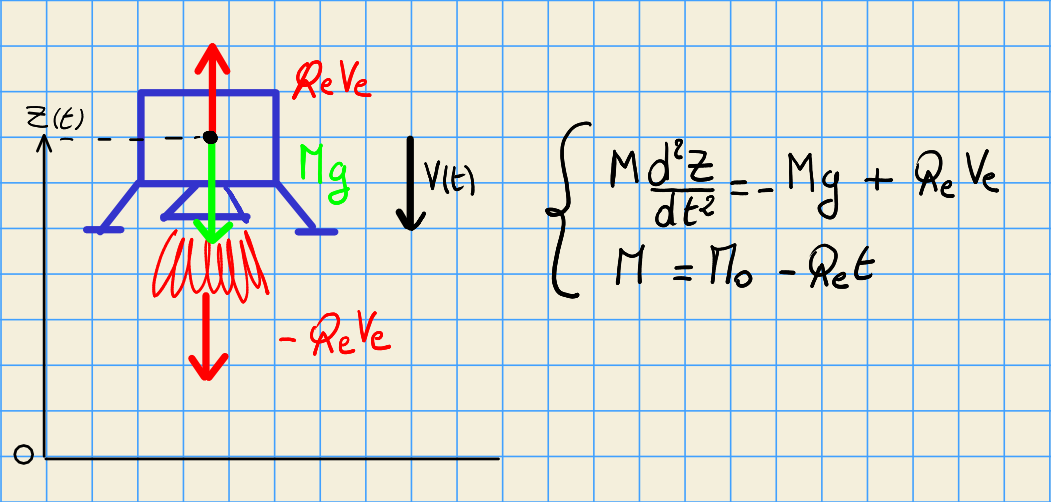
6.2.1.2. modèle mathématique:¶
Equation du mouvement:
en intégrant sur la durée d’une commande \(T\) \(\rightarrow\) vitesse \(V\)
La masse du LEM \(M\) diminue
Approximation par DL car \(X=\frac{Qe*T}{M0} \ll 1\)
d’où l’altitude \(Z\)
expression utilisée dans les premiers programmes en BASIC.
6.2.1.3. cas particuliers¶
Si le fuel est épuisé (\(Qe=0\)), le LEM atteins la surface lunaire au bout d’un temps \(T\) solution de l’équation du 2nd degré:
soit \(T = (-V0 + \sqrt{V0^2 + 2 g Z0})/g\)
Près de la surface, \(T\) trop grand \(\rightarrow\) prédiction \(Z0 < 0\)
calcul \(T\) donnant l’altitude \(Z=0\), solution d’une équation du 6ième degré.
calcul par approximations successives en utilisant un DL de \(Z(t)\)
estimation \(T0\) de \(T\)
\[ T0 = \frac{-V0 + \sqrt{V0^2 + 2 (g-\frac{Ue*Qe}{M0}) Z0}}{g-\frac{Ue*Qe}{M0}} \]recalcule \(V0\) et \(Z0\), puis recommence.
6.2.2. Algorithme: analyse top-down¶
6.2.2.1. problème global¶

6.2.2.2. sous-probleme Lecture_cde¶

6.2.2.3. sous-problème VitesseAltitude¶
applications des formules mathématiques de l’analyse précédente
6.2.2.4. sous-probleme Alunissage¶
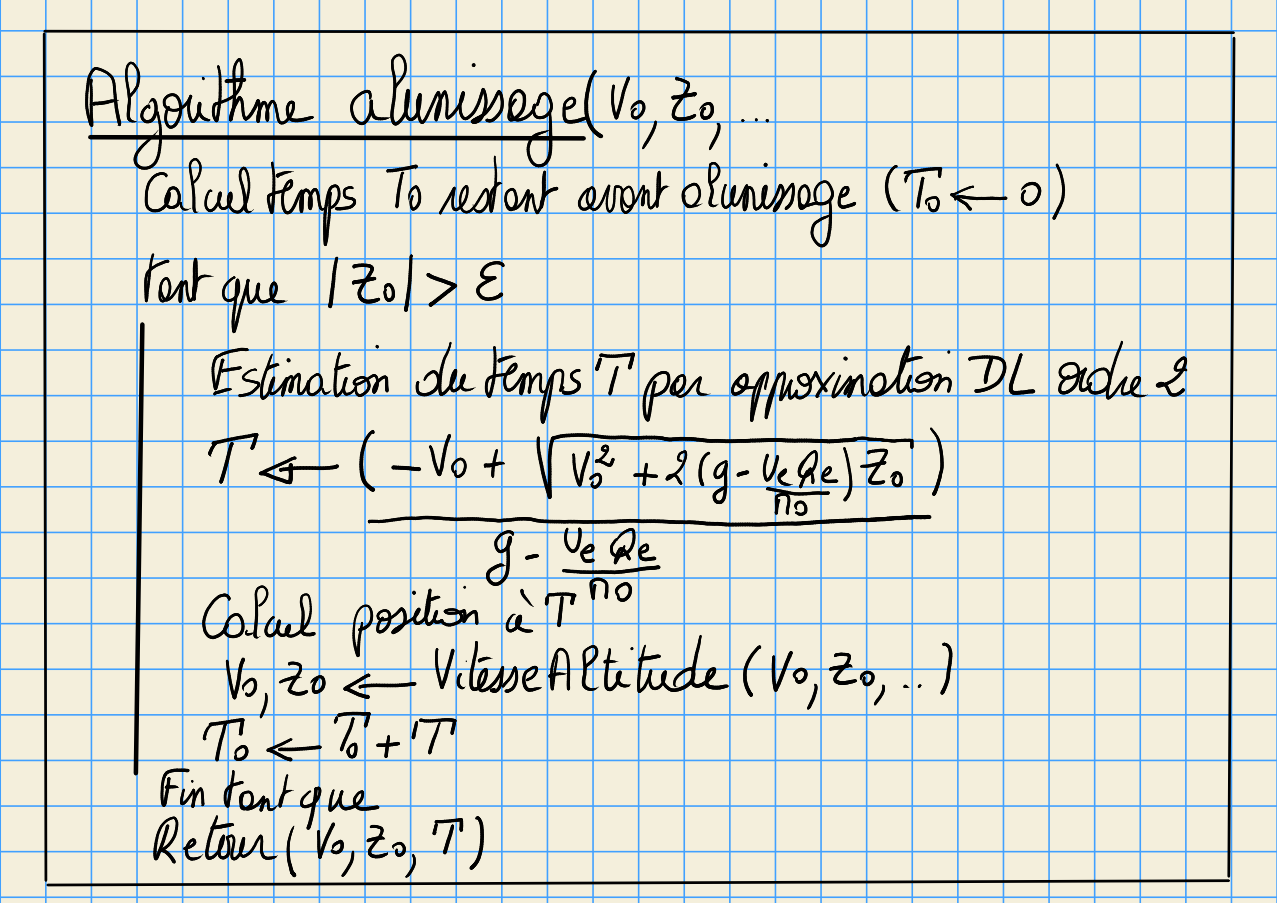
6.2.3. Programmation Python bottom up¶
6.2.3.1. Fonction Lecture_Cde¶
import numpy as np
from random import sample
import sys
# constantes en unité SI (kg/m/s)
g = 1.6 # gravité
Ue = 2900. # vitesse d'ejection
#
def Lecture_Cde(Me,dt):
""" lecture de la commande (poussée) avec test carburant """
T=dt
if Me>0 :
# lecture poussee
# lecture clavier
# ch = input("Entrez la valeur de la poussée (0-100) (en kg/s) = ")[0]
# Qe = int(ch)
# lecture aleatoire
Qe = np.random.randint(100)
# test si reserve de fuel suffisante
if (Me-Qe*T)<0 :
# temps restant d'utilisation du fuel
T = Me/Qe
else:
print("Plus de fuel ")
Qe = 0
# calcul du temps T pour parcourir Z0 (alunissage)
T = (-V0 + np.sqrt(V0*V0 + 2*g*Z0)) / g
return Qe,T
6.2.3.2. Fonction VitesseAltitude¶
def VitesseAltitude(v0,Z0,X,T):
""" calcul de la nvlle vitesse en fonction de la vitesse init V0
un débit sans dimension X=Qe*T/M0 de fuel, pendant un temps T
ainsi que de la nouvelle altitude du LEM
"""
global g,Ue
V = V0 + g*T - Ue*(X + X*X/2. + X**3/3. + X**4/4. + X**5/5.)
Z = Z0 - V0*T - g*T*T/2. + Ue*T*(X/2. + X*X/6. + X**3/12. + X**4/20. + X**5/30.)
return V,Z
6.2.3.3. Fonction Alunissage¶
def Alunissage(V0,Z0,M0,Qe):
""" calcul etat a Z=0 a partir d'une CI V0,Z0,M0 et une poussée Qe """
global g,Ue
# calcul du temps T pour alunissage par approximation successive
T0 = 0
while np.abs(Z0) > 1.e-2:
T= (-V0 + np.sqrt(V0*V0 + 2*(g-Ue*Qe/M0)*Z0)) / (g-Ue*Qe/M0)
V0,Z0 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
T0 = T0+ T
return V0,Z0,T0
6.2.3.4. Programme principal¶
# conditions initiales
Z0 = 190000. # position
V0 = 1580. # et vitesse
M0 = 15000. # masse initiale du LEM
Me = 8000. # dont une masse de fuel
t = 0. # temps simulation
dt = 10. # pas en temps entre chaque commande
#
print("Simulation alunissage")
while np.abs(Z0)>1.e-2 :
Qe,T = Lecture_Cde(Me,dt)
# calcul de la nouvelle position du LEM
V1,Z1 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
# test si alunnissage
if Z1 < 1.e-2 :
V1,Z1,T = Alunissage(V0,Z0,M0,Qe)
# mise a jour de la position du LEM
Z0 = Z1; V0 = V1
Me = Me-Qe*T; M0 = M0-Qe*T
t = t + T
print("t=",int(t),"s Z=",int(Z0),"m V=",int(V0),"m/s fuel=",int(Me),"kg")
# fin simulation
print("Alunissage avec une vitesse ",int(V0)," m/s")
if V0<=0.5 :
print("Alunissage parfait")
elif V0<=5. :
print("Bon alunissage, mais perfectible")
elif V0<=27.:
print("Accident à l'alunissage. Attendez les secours en esperant que vous avez assez d'oxygene !!!")
else :
print("Crash fatal: aucun survivant")
Simulation alunissage
t= 10 s Z= 174927 m V= 1432 m/s fuel= 7180 kg
t= 20 s Z= 160548 m V= 1442 m/s fuel= 7150 kg
t= 30 s Z= 146277 m V= 1411 m/s fuel= 6920 kg
t= 40 s Z= 132230 m V= 1397 m/s fuel= 6780 kg
t= 50 s Z= 118542 m V= 1339 m/s fuel= 6430 kg
t= 60 s Z= 105089 m V= 1351 m/s fuel= 6410 kg
t= 70 s Z= 92169 m V= 1232 m/s fuel= 5800 kg
t= 80 s Z= 79836 m V= 1234 m/s fuel= 5740 kg
t= 90 s Z= 68485 m V= 1033 m/s fuel= 4820 kg
t= 100 s Z= 58659 m V= 931 m/s fuel= 4350 kg
t= 110 s Z= 50099 m V= 779 m/s fuel= 3710 kg
t= 120 s Z= 43126 m V= 613 m/s fuel= 3060 kg
t= 130 s Z= 38142 m V= 379 m/s fuel= 2230 kg
t= 140 s Z= 35310 m V= 184 m/s fuel= 1580 kg
t= 150 s Z= 34322 m V= 11 m/s fuel= 1040 kg
t= 160 s Z= 35893 m V= -333 m/s fuel= 100 kg
t= 165 s Z= 37833 m V= -365 m/s fuel= 0 kg
Plus de fuel
t= 709 s Z= 0 m V= 504 m/s fuel= 0 kg
Alunissage avec une vitesse 504 m/s
Crash fatal: aucun survivant
6.3. Exercice: simulation d’un lancer de balle¶
ou comment programmer le célébre jeux HUNGRY BIRD !

display(Markdown("**Video du cours: Exercice 'Lancer de balle'**"))
YouTubeVideo('QazORncfuIM')
Video du cours: Exercice 'Lancer de balle'
6.3.1. Modèle physique:¶
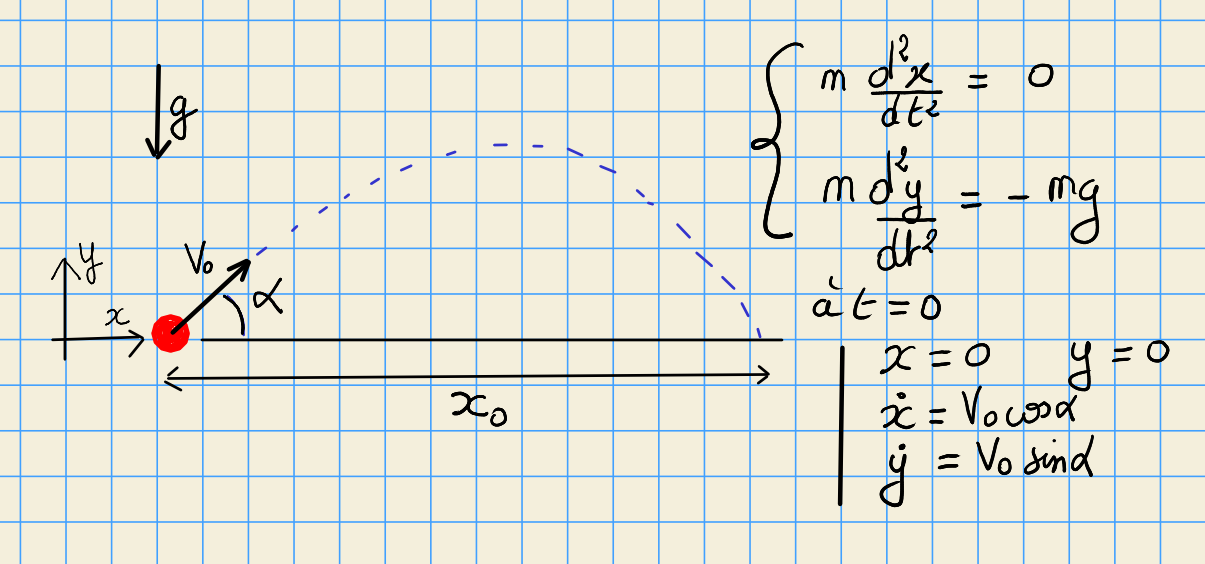
6.3.2. Modèle mathématique:¶
Ce modèle admet une solution analytique simple pour la position \(x_0\)
6.3.3. Objectif du programme¶
Écrire un programme Python qui simule le jeux angry birds en mode texte. On pose un bloc à une distance \(L\) du joueur, qui doit envoyer une balle pour le démolir (i.e. atteindre \(L\) avec une précision donnée).
Le joueur choisit 2 paramètres à valeurs discrètes:
l’angle \(\alpha\) (de 1 à 8 pour un angle de 10 à 45 degré par pas de 5)
la vitesse initiale \(V_0\) (de 1 à 5 par pas 1).
Le joueur a 3 essais, et pour chaque essai, le programme indique la distance atteinte par la balle par rapport au bloc visé.
6.4. Bibliographie¶
Programme originel « Lunar Lander » en Basic sur ATARI:
La programmation structurée (voir aussi l’article fondateur de Dijkstra)
6.5. Fin de la leçon¶

