12. Efficacité / complexité¶

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

12.1. Recherche d’un élément dans un tableau trié¶

Soit X un tableau contenant n valeurs triées, i.e: X[0]<X[1]<…<X[n-1]
on veut déterminer l’indice k d’un élément a, i.e: X[k]=a

12.1.1. algorithme de recherche linéaire¶

on parcours toute la liste en partant du premier élément pour chercher a
dans le pire des cas, on fait n itérations
un test par itération \(\Rightarrow\) n opérations

algorithme avec une efficacité linéaire: \(O(n)\)

def linsearch(a,X):
    """ recherche de  a dans le tableau X 
        retour: valeur de l'indice k tq X[k]=a, ou -1 si non trouvé 
    """
    n = len(X)
    k = -1
    for i in range(n):
        if X[i]==a :
            k = i
            break
    return k
# application
X=np.arange(10)
print(linsearch(5,X))
print(linsearch(10,X))

5
-1

12.1.2. recherche par dichotomie (binary search)¶

on compare a chaque étape la valeur x du milieu du tableau avec a:

si a > x, on recommence avec la moitié droite du tableau
si a < x, on recommence avec la moitié gauche du tableau
si a = x, on termine l’algorithme
par itération: 2 opérations + / et 2 tests
\(\log_2(n)\) itérations au maximum \(\rightarrow\) \(4*\log_2(n)\) opérations

algorithme avec une efficacité logarithmique: \(O(\log(n))\)

def dichotomie(a,X):
    """ recherche de a dans le tableau X 
        renvoie: l'indice k tq a=X(k] ou -1 si non trouvé """
    debut = 0
    fin = len(X)-1
    k = -1
    while (debut<=fin) and (k<0):
        milieu = (debut+fin)//2
        if X[milieu]==a :
            k = milieu
            break
        elif X[milieu]>a :
            fin = milieu
        else:
            debut = milieu
    return k
# application
X=np.arange(10)
print(dichotomie(5,X))

remarque: le programme précédent possède une erreur, car il est non générique !!

Pouvez vous la trouver et la corriger ?
(Conseil:) essayer dichotomie(10,X) !

12.1.3. comparaison de l’efficacité des 2 algorithmes de trie¶

run courbe1.py

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

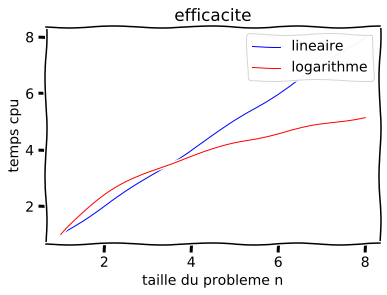
\(\Rightarrow\) pour n grand l’algorithme de trie par bisection est beaucoup plus efficace

12.2. Complexité et efficacité d’un algorithme¶

théorie de la complexité: analyse d’un algorithme en vue de déterminer les ressources nécessaire (en temps CPU, en taille mémoire,..) pour l’exécuter en fonction des données (taille des données, paramètre de précision).

efficacité = estimation asymptotique de la complexité en temps sur une machine idéale (machine de Turing) en fonction d’un paramètre n caractérisant les entrées (taille des entrées, nbre de digits pour la précision,..)

attention cette analyse n’est qu’indicative, et peut être remise en question suivant l’architecture des machines (machines parallèles)

12.2.1. Différentes classes de compléxité (classées par efficacité)¶

type	complexité	example
constante	\(O(1)\)	accés à un tableau: X[i]
logarithmique	\(O(\log{n})\)	trie par dichotomie (binary search)
linéaire	\(O(n)\)	parcours de tableaux
linéarithmique	\(O(n\log{n}\)	methode multigrille
quadratique	\(O(n^2)\)	produit matrice x vecteur
cubique	\(O(n^3)\)	produit matrice x matrice
exponentielle	\(O(2^{n^p})\)
factorielle	\(O(n!)\)	calcul déterminant d’une matrice (force brute)

run courbe2.py

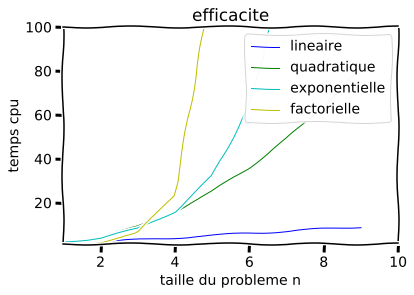
12.3. Exemples¶

12.3.1. algorithme inefficace: déterminant de Cramer¶

Calcul du déterminant d’une matrice \(A\) par la méthode de Cramer

formule récursive de calcul par développement par rapport à la première colonne

\[ det(A) = \sum_{j=1}^n A_{1,j} (-1)^{1+j} det(A^{1,j}) \]

\(A^{1,j}\) matrice d’ordre n-1 obtenue en enlevant la colonne 1 et la ligne i de \(A\)
calcul det(A) = somme de n déterminants d’ordre (n-1)

\(\Rightarrow\) algorithme avec une efficacité factorielle: \(O(n!)\)

# nbre d'operations
nops = 0
# algorithme déterminant
def determinant(A):
    """ Calcul du déterminant de A """
    global nops
    n=shape(A)[0]
    if n==1:
        return A[0,0]
    else:
        det =0.0
        coef=1.0
        # developement par rapport a la ligne 0
        for i in range(n):
            A1 = delete(delete(A,0,0),i,1)
            det = det + coef*A[0,i]*determinant(A1)
            coef = -coef
        nops += 3*n
        return det
# test d'utilisation avec timing
from time import process_time
N=range(5,10)
# boucle de timing 
for k,n in enumerate(N):
    A=random.rand(n,n)
    nops = 0
    debut= process_time()
    det1 = determinant(A)
    cpu  = process_time() - debut
    print("n=%d nops=%10d cpu=%12.6g s"%(n,nops,cpu))

n=5 nops=       615 cpu=   0.0167587 s
n=6 nops=      3708 cpu=   0.0892365 s
n=7 nops=     25977 cpu=      0.4512 s

n=8 nops=    207840 cpu=     2.50121 s

n=9 nops=   1870587 cpu=     22.3046 s

\(\Rightarrow\) algorithme inutilisable !!!!
\(\Rightarrow\) utiliser l’algorithme de la bibliothéque numpy basé sur une factorisation \(LU\) de \(A\)

print(shape(A))
%timeit linalg.det(A)

(9, 9)

18.2 µs ± 88.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

12.3.2. Exemple: recherche de la racine d’une fonction¶

Calcul d’une valeur approchée \(x^n\) de la racine \(x^*\) d’une fonction \(f(x)\):

\[ \left| x^* - x^n \right| < \epsilon \mbox{ avec } f(x^*)=0 \]

Le nombre de chiffres significatifs \(P\) de \(x^n\) est donnée par \(P= -\log(\epsilon)\)
On compare l’efficacité de 2 algorithmes en fonction de \(P\)
On suppose que l’on a un intervalle \([a,b]\) contenant la racine \(x^*\)

12.3.2.1. Méthode de dichotomie¶

algorithme itératif de dichotomie
on choisit comme approximation le milieu de l’intervalle
à chaque itération: erreur divisée par 2 , 4 opérations + 1 appel de fonction \(\Rightarrow\) erreur divisée par \(2^n\) au bout de n iterations

efficacité linaire \(O(P)\) car le coût \(\approx C*P + K \)

# Algorithme Dichotomie
def Dichotomie(F,a,b,eps):
    """ calcul la racine de F(x) comprise entre a et b par dichotomie
        F(x) est une fonction , eps = précision """
    nit = 0
    ya = F(a)
    yb = F(b)
    x  = (a+b)/2.0
    while (b-a)>eps :
        x = (a+b)/2.
        y = F(x)
        if y*ya > 0:
            a=x
            ya=y
        else:
            b=x
            yb=y
        nit = nit + 1
    return x,nit
# application
F = cos
xs = pi/2.
x,it = Dichotomie(F,pi/3,3*pi/4,1.e-08)
print("racine %g  nit=%d  err=%g"%(x,it,abs(x-xs)))

racine 1.5708  nit=27  err=1.95056e-09

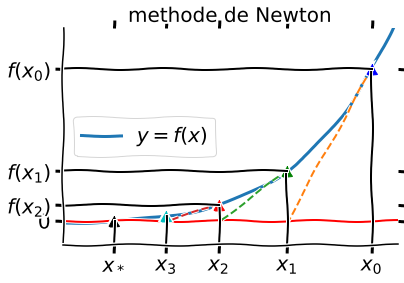
12.3.2.2. Méthode de Newton¶

à partir de \(x_0\), on approxime la courbe par sa tangente en \(x_0\)
nouvelle approximation \(x_1\) = intersection tangente avec l’axe des x

\[ x_1 = x_0 - \frac{F(x_0)}{F'(x_0)}\]

l’erreur \(err_1 = x_1 -x^*\) vérifie après D.L. de \(F(x_0)\)

\[ err_1 = err_0 - \frac{F(x_0)}{F'(x_0)} \approx \frac{1}{2}\frac{F''(x_0)}{F'(x_0)}({err_0})^2 + ..\]

soit au bout de \(n\) itérations \(err_n \approx (err_0)^{2^n} \)

Efficacité logarithmique \(O(\log P)\) car coût \(\approx C \log P + K\)

run newton.py

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

# Algorithme de Newton
def Newton(F,dF,a,b,eps):
    """ calcul la racine de F(x) par la methode de Newton
        F(x) fonction, dF dérivée, a b intervalle d'étude , eps = précision """
    nit = 0
    x   = (a+b)/2.
    err = F(x)/dF(x)
    while abs(err) > eps:
        x   = x - err
        err = F(x)/dF(x)
        nit = nit + 1
    return x,nit
# application
F  = lambda x:  cos(x)
dF = lambda x: -sin(x)
xs = pi/2.
x,it = Newton(F,dF,pi/3,3*pi/4,1.e-08)
print("racine %g  nit=%d  err=%g"%(x,it,abs(x-xs)))

racine 1.5708  nit=2  err=1.42208e-10

12.3.2.3. Conclusion¶

La méthode de Newton est beaucoup plus efficace que la méthode de dichotomie
Attention cependant, la convergence de la méthode de Newton est uniquement locale !!!

INPROS INtroduction à la PROgrammation Scientifique en Python

Efficacité / complexité

Contenu